Simple Random Walk
Simple Random Walk simulation in Python.
Introducción
La caminata aleatoria en \(\mathbb{Z}\), es la más simple de todas, de ahí su nombre. \(X_1\) toma valores en \(\{-1; 1\}\), y la caminata comienza en \(0\) y está definida para valores en \(\mathbb{Z}\). Las probabilidades se denotan como:
$$\begin{equation}
P(X_1 = 1) = P(X_1 = -1) = 1/2
\end{equation}$$
Considerando el caso más general, se tiene que
$$\begin{equation}
P(X_1 = 1) = p \ \ y \ \ P(X_1 = -1) = 1 - p
\end{equation}$$
Vamos a obtener la probabilidad de que el caminante se encuentre en
la posición \(m\) después de \(N\) pasos. Para \(m < N\) hay muchas maneras de empezar en \(0\) y pasar por \(N\) saltos a sitios vecinos más cercanos y terminar en \(m\). Sabemos que el número de pasos viene dado por la posición final más el número de pasos a la izquierda, es decir, \(n_1 = m + n_2\), y a parte sabemos que \(n_1 + n_2 = N\), solucionando para \(n_1\) y \(n_2\), se tiene
$$\begin{equation}
n_1 = \frac{1}{2} (N + m) \\
n_2 = \frac{1}{2} (N - m) \\
\end{equation}$$
La probabilidad de una secuencia de saltos a la izquierda y a la derecha es el producto de las probabilidades de los saltos individuales. Como los saltos individuales son independientes, todos los caminos que empiezan en \(0\) y terminan en \(m\) tienen la misma probabilidad global.
$$\begin{equation}
p^{n_1} q^{n_2} = p^{\frac{1}{2} (N + m)} q^{\frac{1}{2} (N + m)}
\end{equation}$$
Esta probabilidad debe multiplicarse por el número total de trayectorias con \(n_1\) pasos a la derecha y \(n_2\) pasos a la izquierda. Esto viene dado por el número de formas de poner \(n_1\) objetos de \(N\) en una caja y \(n_2 = N - n_1\) objetos en otra caja. El primer objeto se puede elegir de \(N\) maneras,
el segundo de \(N - 1\) maneras y así sucesivamente. Por lo tanto, el número total de elección de \(n_1\) objetos es \(N(N - 1)(N - 2)(N - n_1 - 1)\). Pero los \(n_1\) objetos son idénticos y pueden disponerse en cualquier orden.
$$\begin{equation}
\frac{N!}{n_1! n_2!} = \frac{N!}{n_1!(N-n_1)!}
\end{equation}$$
La probabilidad de estar en la posición m después de \(N\) saltos viene dada, por
$$\begin{equation}
p(m, N) = \frac{N!}{\left(\frac{N+m}{2}\right)! \left(\frac{N-m}{2}\right)!} p^{\frac{1}{2} (N + m)} q^{\frac{1}{2} (N - m)}
\end{equation}$$
Si conocieramos la distribución de probabilidad podr?amos obtener todos los
momentos. Note que la ecuación anterior se parece mucho a la distribución binomial, si consideramos el n?mero de pasos hacia la derecha como \(n = (N +m)/2\) podemos escribir
$$\begin{equation}
p(n, N) = \frac{N!}{n! (N-n)!} p^{n} q^{N - m}
\end{equation}$$
Suponemos que ya conocemos los momentos de la distribución binomial, entonces
$$\begin{equation}
E[n] = NP \\
Var(n) = Npq
\end{equation}$$
Como \(n = (N + m)/2! \rightarrow m = 2n - N\), el valor esperado de la posición del caminante después de \(N\) pasos viene dada ahora por
$$\begin{eqnarray}
E[m] & = & 2E[n] - N \\
& = & 2Np - N \\
& = & N(2p - 1)
\end{eqnarray}$$
y la varianza viene dada por
$$\begin{eqnarray}
Var[m] & = & 4Var(n) \\
& = & 4Npq
\end{eqnarray}$$
Simulación
# Reading packages
library("ggplot2")
library("dplyr")
library("plotly")
library("ggthemes")
library("tidyr")
library("stringr")
# Función para simular una caminata aleatoria simple
simple.random.walk <- function(n.steps, n.sim, prob.r=0.5){
n <- n.steps
a <- prob.r
# movimiento
x.left = -1
x.right = 1
# iteración
Sn_mat <- matrix(0,ncol=n+1,nrow=n.sim)
for(i in 1:n.sim){
for(j in 2:(n+1)){
step <- sample(c(x.left,x.right), 1, prob=c(1-a,a), replace=F)
Sn_mat[i,j] <- Sn_mat[i,j-1] + step
}
}
# names
names <- sapply(1:(n+1),function(i) paste('step',i,sep=''))
# data frame
result_df <- data.frame('sim'=sapply(1:n.sim, function(i) paste('sim',i,sep='')),
'Sn'=Sn_mat)
return(result_df)
}
Caminata aleatoria simple (1-D)
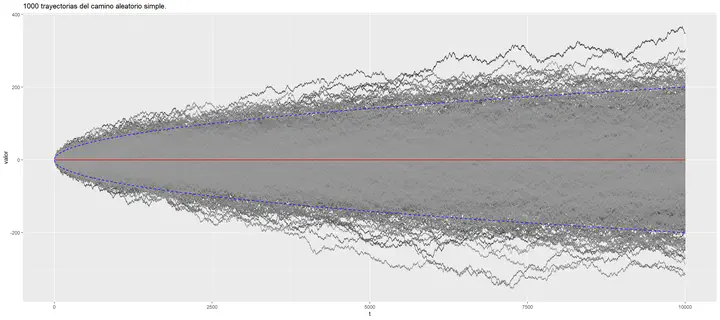
Ejemplo 1: \(p = 0.5\)
####### Ejemplo:
n.steps <- 10000 # número de pasos
n.sim <- 1000 # número de trayectorias
p <- 0.5 # probabilidad de moverse a la derecha
df <- simple.random.walk(n.steps, n.sim, prob.r=p)
## trayectorias
df_rw <- df %>%
gather(key='t',value='valor',-sim) %>%
mutate(t = as.numeric(substring(t,4,10))) %>%
arrange(sim)
# valores teóricos
moments_rw <- data.frame('t'=c(1:n.steps),'p'=p) %>%
mutate('mean'=t*(p-(1-p)),
'sd_sup'=mean + 2*sqrt(4*t*p*(1-p)),
'sd_inf'=mean - 2*sqrt(4*t*p*(1-p)))
# gráfico
p1 <- ggplot(df_rw,aes(x=t,y=valor,color=sim)) +
geom_line() +
geom_line(moments_rw, mapping=aes(x=t,y=mean),col='red',size=0.7) +
geom_line(moments_rw, mapping=aes(x=t,y=sd_sup),col='blue',size=0.7,linetype = "dashed") +
geom_line(moments_rw, mapping=aes(x=t,y=sd_inf),col='blue',size=0.7,linetype = "dashed") +
scale_colour_grey(start = 0.2,end = 0.6) +
theme(legend.position="none") +
ggtitle(paste(n.sim," trayectorias del camino aleatorio simple.",sep=''))
p1

Ejemplo 2: \(p = 0.6\)
####### Ejemplo
n.steps <- 10000 # número de pasos
n.sim <- 1000 # número de trayectorias
p <- 0.6 # probabilidad de moverse a la derecha
df <- simple.random.walk(n.steps, n.sim, prob.r=p)
# trayectorias
df_rw <- df %>%
gather(key='t',value='valor',-sim) %>%
mutate(t = as.numeric(substring(t,4,10))) %>%
arrange(sim)
# valores teóricos
moments_rw <- data.frame('t'=c(1:n.steps),'p'=p) %>%
mutate('mean'=t*(p-(1-p)),
'sd_sup'=mean + 2*sqrt(4*t*p*(1-p)),
'sd_inf'=mean - 2*sqrt(4*t*p*(1-p)))
#gráfico
p2 <- ggplot(df_rw,aes(x=t,y=valor,color=sim)) +
geom_line() +
geom_line(moments_rw, mapping=aes(x=t,y=mean),col='red',size=0.7) +
geom_line(moments_rw, mapping=aes(x=t,y=sd_sup),col='blue',size=0.7,linetype = "dashed") +
geom_line(moments_rw, mapping=aes(x=t,y=sd_inf),col='blue',size=0.7,linetype = "dashed") +
scale_colour_grey(start = 0.2,end = 0.6) +
theme(legend.position="none") +
ggtitle(paste(n.sim," trayectorias del camino aleatorio simple.",sep=''))
p2

Ejemplo 3: \(p = 0.4\)
####### Ejemplo
n.steps <- 10000 # número de pasos
n.sim <- 1000 # número de trayectorias
p <- 0.4 # probabilidad de moverse a la derecha
df <- simple.random.walk(n.steps, n.sim, prob.r=p)
# trayectorias
df_rw <- df %>%
gather(key='t',value='valor',-sim) %>%
mutate(t = as.numeric(substring(t,4,10))) %>%
arrange(sim)
# valores teóricos
moments_rw <- data.frame('t'=c(1:n.steps),'p'=p) %>%
mutate('mean'=t*(p-(1-p)),
'sd_sup'=mean + 2*sqrt(4*t*p*(1-p)),
'sd_inf'=mean - 2*sqrt(4*t*p*(1-p)))
# gráfico
p3 <- ggplot(df_rw,aes(x=t,y=valor,color=sim)) +
geom_line() +
geom_line(moments_rw, mapping=aes(x=t,y=mean),col='red',size=0.7) +
geom_line(moments_rw, mapping=aes(x=t,y=sd_sup),col='blue',size=0.7,linetype = "dashed") +
geom_line(moments_rw, mapping=aes(x=t,y=sd_inf),col='blue',size=0.7,linetype = "dashed") +
scale_colour_grey(start = 0.2,end = 0.6) +
theme(legend.position="none") +
ggtitle(paste(n.sim," trayectorias del camino aleatorio simple.",sep=''))
p3

Caminata aleatoria simple (2-D)
# Caminata aleatoria simple en dos dimensiones
randomWalk2d_plot <- function(base, n.steps){
df <- base
df_2d <- df %>%
gather(key='t',value='valor',-sim) %>%
filter(sim == 'sim1' | sim=='sim2') %>%
spread(sim,valor) %>%
mutate(t = as.numeric(substring(t,4,10))) %>%
arrange(t) %>%
filter(t <= n.steps)
b2 <- ggplot(df_2d,aes(x=sim1,y=sim2))+
geom_point(color="blue") +
geom_point(df_2d%>%filter(t == 1),mapping=aes(x=sim1,y=sim2),color="green") +
geom_point(df_2d%>%filter(t == max(t)),mapping=aes(x=sim1,y=sim2),color="red") +
geom_path() +
theme(axis.title.x = element_blank(),
axis.title.y = element_blank(),
axis.text.x=element_blank(),
axis.text.y=element_blank(),
axis.ticks.x=element_blank(),
axis.ticks.y=element_blank())
return(b2)
}
Ejemplo 1:
# valores iniciales
n.steps <- 10000 # numero de pasos
n.sim <- 1000 # n?mero de trayectorias
p <- 0.5 # probabilidad de moverse a la derecha
# Gr?fico
df <- simple.random.walk(n.steps,n.sim,prob.r=p)
b4 <- randomWalk2d_plot(df, n.steps)
b4
