Introducción

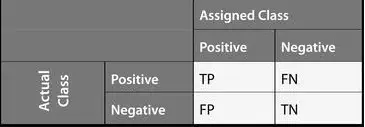
La matriz de confusión se utiliza como indicador en temas de clasificación. Contiene el número de elementos que se han sido clasificados correcta o incorrectamente para cada clase. En su diagonal diagonal principal el número de observaciones correctamente clasificadas para cada clase, los elementos no diagonales indican el número de observaciones incorrectamente clasificadas. Una de las ventajas de una matriz de confusión es que es fácil ver si el un modelo u algoritmo confunde dos clases.

La matriz de confusión puede aplicarse tanto a la clasificación binaria como a los problemas de clasificación multiclase. La salida TN significa Verdadero Negativo y muestra el número de ejemplos negativos clasificados con precisión. Del mismo modo, TP significa Verdadero Positivo, que indica el número de ejemplos positivos clasificados con precisión. El término FP muestra el valor Falso Positivo, es decir, el número de ejemplos negativos reales clasificados como positivos; y FN significa un valor Falso Negativo que es el número de ejemplos positivos reales clasificados como negativos.

La matriz de confusión consta de cuatro características básicas (números) que se utilizan para definir la métrica de medición del clasificador. Estos cuatro números son:

1. TP (Verdadero Positivo): Por ejempo, TP representa el número de ejemplos que se ha clasificado como positivos cuando son positivos.

2. TN (Verdadero Negativo): TN representa el número de ejemplos clasificados como negativos cuando en realidad lo son.

3. FP (Falso Positivo): FP representa el número de ejemplos clasificados erróneamente como positivos cuando en realidad son negativos. FP también se conoce como error de tipo I.

4. FN (Falso Negativo): FN representa el número de ejemplos clasificados erróneamente como negativos cuando en realidad son positivos. FN también se conoce como error de tipo II.

De la matriz de confusión se pueden definir las siguientes métricas: Las métricas de rendimiento de un algoritmo son: accuracy, precision, recall, y el F1 score, que se calculan a partir de los valores TP, TN, FP y FN mencionados anteriormente.

Accuracy

El accuracy se representa como la relación entre ejemplos clasificados correctamente (TP+TN) y el número total de ejemplos (TP+TN+FP+FN).

$$\begin{equation} Accuracy = \frac{(TP + TN)}{(TP + FP + FN + TN)} \end{equation}$$

Precision

La precisión se representa como la relación entre ejemplos correctamente clasificados positivos (TP) y el total de pacientes a los que se predice como positivos (TP+FP). Mide que tan preciso es un modelo entre los predichos positivos.

$$\begin{equation} Precision = \frac{(TP)}{(TP + FP)} \end{equation}$$

Recall

La métrica recall se define como la proporción de ejemplos correctamente clasificados (TP) dividida por el número total de ejemplos que tienen realmente son positivos.

$$\begin{equation} Recall = \frac{(TP)}{(TP + FN)} \end{equation}$$

El Recall es también conocido como sensitivity.

F1 score

La métrica \(F1 \ score\) también se conoce como \(F\ measure\). La métrica \(F1\ score\) establece el equilibrio entre la precision y recall. En términos prácticos esta medida busca un balance entre precision y recall.

$$\begin{equation} F1\ score = 2 \times \frac{Precision \times Recall}{Precision + Recall} \end{equation}$$

Ejemplo:

Breast Cancer dataset

Descripción del conjunto de datos

Las características se obtivieron a partir de una imagen digitalizada de un aspirado con aguja fina (AAF) de una masa mamaria.

El plano de separación descrito anteriormente se obtuvo mediante el método Multisurface Method-Tree (MSM-T). Las características relevantes se seleccionaron mediante una búsqueda exhaustiva en el espacio de 1-4 características y 1-3 planos de separación.

Atributos:

• radio (media de las distancias del centro a los puntos del perómetro)
• textura (desviación estándar de los valores de la escala de grises)
• perímetro
• área
• suavidad (variación local de las longitudes de los radios)
• compacidad ($perímetro^2$ / área - 1)
• concavidad (gravedad de las partes cóncavas del contorno)
• puntos cóncavos (número de porciones cóncavas del contorno)
• simetría
• dimensión fractal (“aproximación de la línea de costa” - 1)

Referencia:

“Breast Cancer Wisconsin (Diagnostic) Data Set”

from sklearn.linear_model import LogisticRegression
from sklearn import datasets
from sklearn.metrics import confusion_matrix
from sklearn.model_selection import cross_val_predict
from sklearn.model_selection import train_test_split
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()

# datos
bcancer = datasets.load_breast_cancer()

División de los datos

Separamos los datos en conjuntos de entrenamiento (training) y conjunto de prueba (testing).

bcancer = datasets.load_breast_cancer()

X = bcancer['data']
y = bcancer['target']

# Split data
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=42, stratify=y)
print(X_test.shape)

## (171, 30)

Modelo

Ajustamos un modelo simple, el de regresión logística.

lr = LogisticRegression(random_state=42, solver='lbfgs', max_iter=7600)
lr.fit(X_train, y_train)
# prediction

## LogisticRegression(max_iter=7600, random_state=42)

y_pred = lr.predict(X_test)

Obtenemos la matriz de confusión

# confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)

pd.DataFrame(conf_matrix,
             columns = pd.MultiIndex.from_product([['Prediction'], ['Negative', 'Positive']]),
             index = pd.MultiIndex.from_product([['Actual'], ['Negative', 'Positive']]))

##                 Prediction         
##                   Negative Positive
## Actual Negative         57        7
##        Positive          2      105

labels= ['malignant', 'benign']
plt.figure(figsize=(8, 6))
sns.heatmap(conf_matrix, xticklabels=labels, yticklabels=labels, annot=True, fmt="d");
plt.title("Confusion matrix")
plt.ylabel('True class')
plt.xlabel('Predicted class')
plt.show()

De lo anterior podemos concluir que el modelo es bueno ya que predice de \(105\) casos (en el conjunto de prueba, testing) de un total de \(179\) como cáncer benigno cuando en realidad es cáncer benigno, por otro lado, predice \(56\) casos como cáncer maligno cuando en realidad es cáncer maligno. Como lo valores de los falsos tanto positivos como negativos son muy bajos, es de esperar que las métricas sean altas.

from sklearn.metrics import accuracy_score, recall_score, precision_score, f1_score

# accuracy
accuracy = accuracy_score(y_test, y_pred)
print('Accuracy: {}'.format(accuracy))
# precision

## Accuracy: 0.9473684210526315

precision = precision_score(y_test, y_pred)
print('Precision: {}'.format(precision))
# recall

## Precision: 0.9375

recall = recall_score(y_test, y_pred)
print('Recall: {}'.format(recall))
# f1 score

## Recall: 0.9813084112149533

f1score = f1_score(y_test, y_pred)
print('F1 score: {}'.format(f1score))

## F1 score: 0.958904109589041

from sklearn.metrics import roc_curve, auc

xylim = [-0.1, 1.1]
plt.figure(figsize=(12,7))
preds_train = lr.predict(X_train)
# calculate prediction probability
prob_train = np.squeeze(lr.predict_proba(X_train)[:,1].reshape(1,-1))
prob_test = np.squeeze(lr.predict_proba(X_test)[:,1].reshape(1,-1))
# false positive rate, true positive rate, thresholds
fpr1, tpr1, thresholds1 = roc_curve(y_test, prob_test)
fpr2, tpr2, thresholds2 = roc_curve(y_train, prob_train)
# auc score
auc1 = auc(fpr1, tpr1)
auc2 = auc(fpr2, tpr2)
# plot auc 
plt.plot(fpr1, tpr1, color='blue', label='Test ROC curve area = %0.2f'%auc1)
plt.plot(fpr2, tpr2, color='green', label='Train ROC curve area = %0.2f'%auc2)
plt.plot([0,1],[0,1], 'r--')
plt.xlim(xylim)

## (-0.1, 1.1)

plt.ylim(xylim)

## (-0.1, 1.1)

plt.title('Curva ROC')
plt.xlabel('False Positive Rate', size=14)
plt.ylabel('True Positive Rate', size=14)
plt.legend(loc='lower right')
plt.show()